December 2021

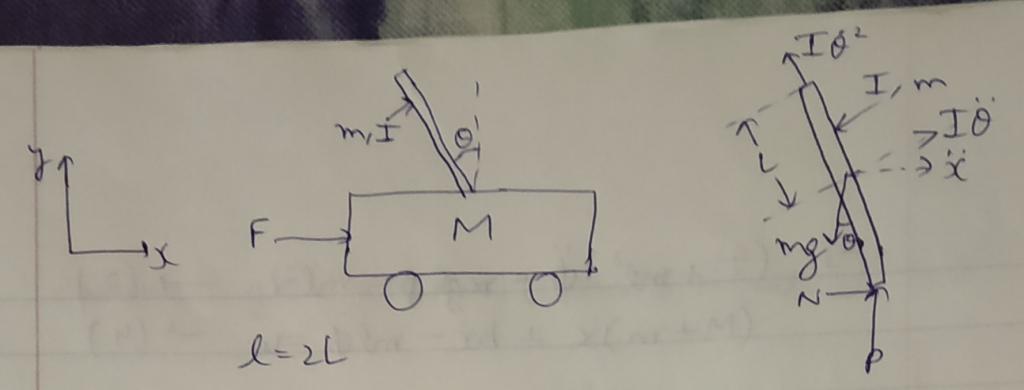
Motivation: Class Project

Objective: Stabilizing linearized dynamics of a Single Inverted Pendulum on a cart in 2D

Details: MATLAB was used to implement the solution.

Steps followed:

1. Derive the non-linear dynamical equations using Newtonian method (Force approach)
2. Linear the dynamics by assuming that the pendulum movement is infinitesimal.
3. Convert the equations into state-space equations and observe the output which is unstable
4. Apply State Feedback Control Law ( A’ = A – B*K) and observe the output which is stable

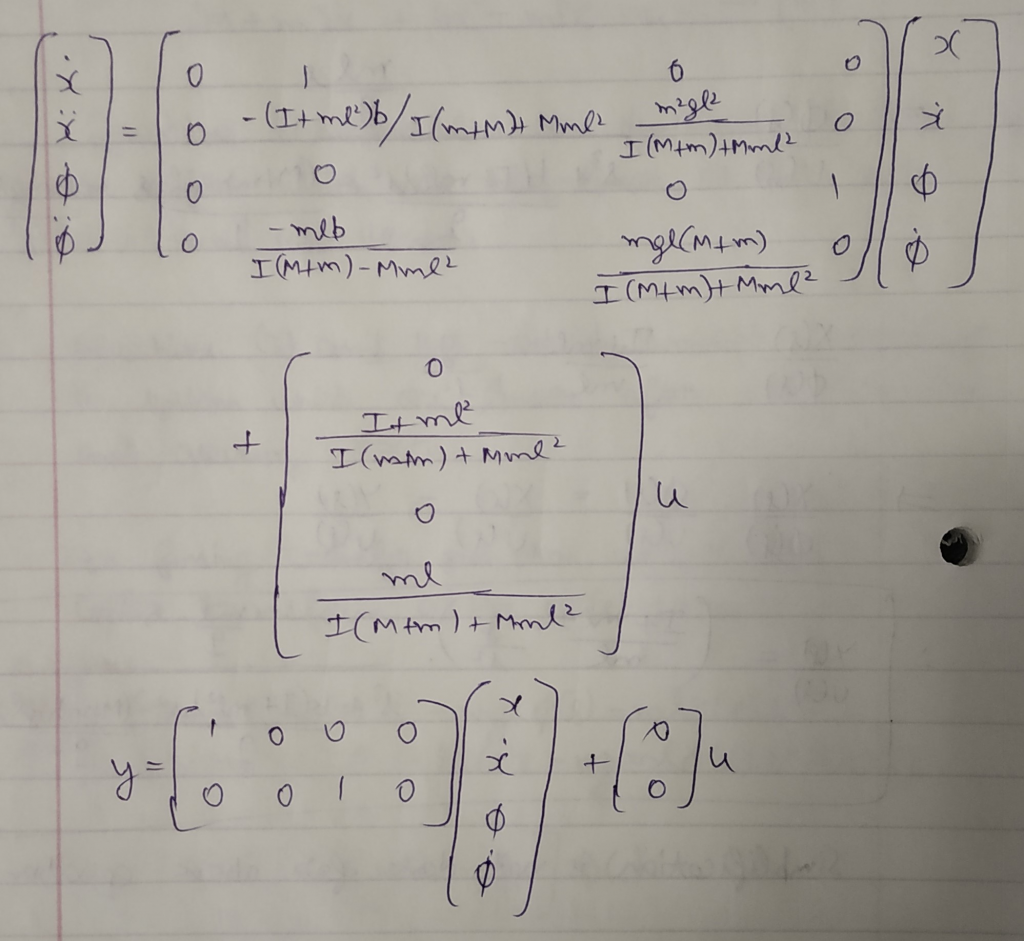
Equations (1) and (2) are the non-linear equations of motion whereas (3) and (4) are the linearized equations of motion using the above assumption. Upon converting the linearized equations to state space using algebraic manipulation, we get below.

M = 2;
m = 0.1;
b = 0.1;
g = 9.8;
l = 0.25;
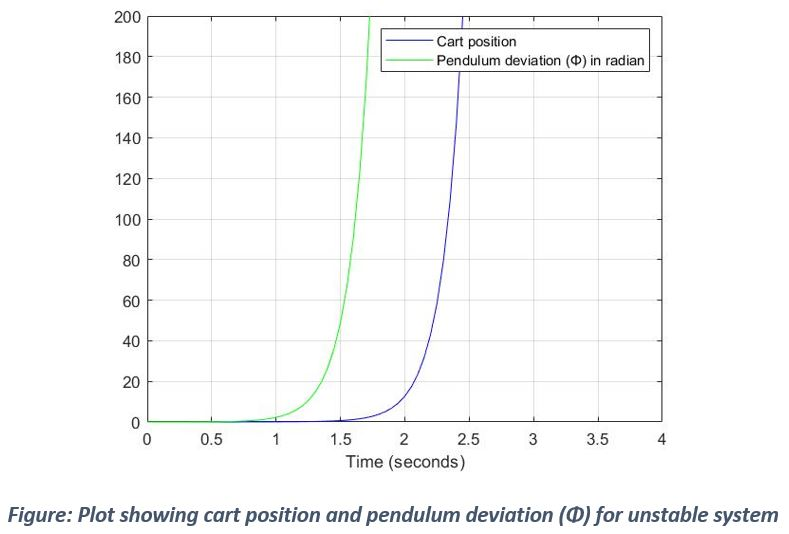
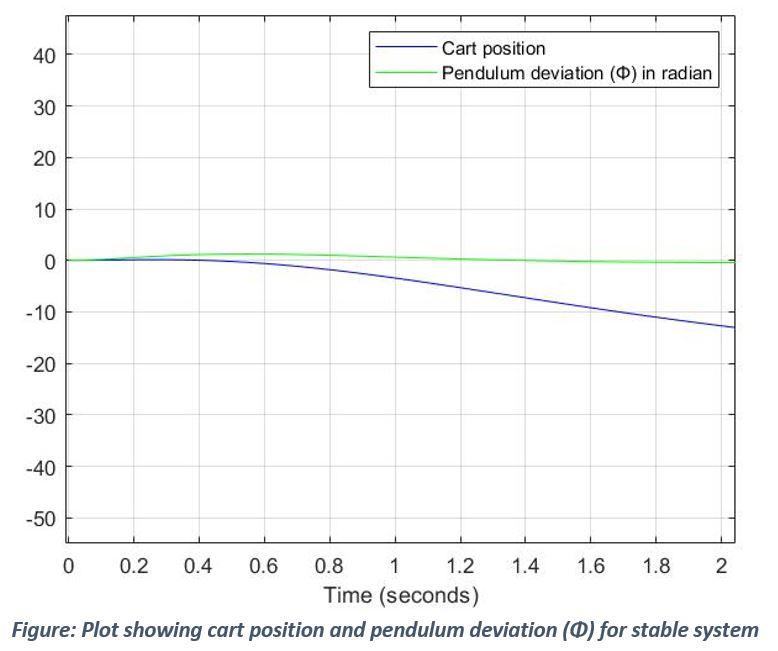
i = (m*l*l)/12;

For the below set of system parameters, eigen value of A matrix are 0, -0.0476, -6.1532, and 6.1510 all of which are not negative (0 and 6.1510) which contribute to system unstability. For some force input to the system, we get a below response which in unstable. If eigen values are changes using MATLAB’s place function (K = place(A, B, [ -1 -2 -3 -4])) and Adash = A – (B*K); we get a stable system response because all the eigen values are strictly negative.

Analysis:

Unstable response: From the figure, it can be inferred that as cart moves, deviation of pendulum also increases to a reasonably high value which means that it is not held upright and falls down.

Stable response: From the figure, it can be inferred that as cart moves, pendulum deviation (Φ) is very close to zero as expected. As a result, pendulum does not drops down and stays upright.